dp问题
满足最优子结构:不管过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。
无后效性:以前各阶段的状态无法直接影响它未来的决策。
背包问题
有 N件物品和一个容量是 V的背包。每件物品只能使用一次。
第 i 件物品的体积是 v_i,价值是 w_i。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 v_i, w_i,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<vi,wi≤1000

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #include <iostream>
using namespace std;
int n,m;
int w[1010],v[1010];
int f[1010][1010];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>w[i]>>v[i];
}
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
if(j<w[i]) f[i][j]=f[i-1][j];
else{
f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
}
}
}
cout<<f[n][m];
return 0;
}
|
当每种类别有s个物品,多重背包问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| #include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int f[N][N]={};
int s[N],v[N],w[N];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i]>>s[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=1;k<=s[i];k++){
if(j<k*v[i]) f[i][j]=f[i-k][j];
else f[i][j]=max(f[i-1][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
cout<<f[n][m];
return 0;
}
|
摘花生
Hello Kitty想摘点花生送给她喜欢的米老鼠。
她来到一片有网格状道路的矩形花生地(如下图),从西北角进去,东南角出来。
地里每个道路的交叉点上都有种着一株花生苗,上面有若干颗花生,经过一株花生苗就能摘走该它上面所有的花生。
Hello Kitty只能向东或向南走,不能向西或向北走。
问Hello Kitty最多能够摘到多少颗花生。
输入格式
第一行是一个整数T,代表一共有多少组数据。
接下来是T组数据。
每组数据的第一行是两个整数,分别代表花生苗的行数R和列数 C。
每组数据的接下来R行数据,从北向南依次描述每行花生苗的情况。每行数据有C个整数,按从西向东的顺序描述了该行每株花生苗上的花生数目M。
输出格式
对每组输入数据,输出一行,内容为Hello Kitty能摘到得最多的花生颗数。
数据范围
1≤T≤100
,
1≤R,C≤100
,
0≤M≤1000

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| #include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int f[N][N];
int a[N][N];
int n,m;
int main(){
int t;
cin>>t;
while(t--){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<m;j++){
f[i][j]=max(f[i-1][j],f[i][j-1])+a[i][j];
}
}
cout<<f[n-1][m-1]<<endl;
}
return 0;
}
|
偷商店
阿福是一名经验丰富的大盗。趁着月黑风高,阿福打算今晚洗劫一条街上的店铺。
这条街上一共有 N 家店铺,每家店中都有一些现金。
阿福事先调查得知,只有当他同时洗劫了两家相邻的店铺时,街上的报警系统才会启动,然后警察就会蜂拥而至。
作为一向谨慎作案的大盗,阿福不愿意冒着被警察追捕的风险行窃。
他想知道,在不惊动警察的情况下,他今晚最多可以得到多少现金?
输入格式
输入的第一行是一个整数 T,表示一共有 T 组数据。接下来的每组数据,第一行是一个整数 N ,表示一共有 N 家店铺。第二行是 N 个被空格分开的正整数,表示每一家店铺中的现金数元。
每家店铺中的现金数量均不超过1000。
imput tamples:
2
3
1 8 2
4
10 7 6 14
result:
8
24
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| #include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int rob(vector<int>& money){
int dp[200]={};
dp[0]=money[0];
int n=money.size();
for(int i=1 ;i<n;++i){
if(i==1){
dp[1]=max(money[0],money[1]);
}
else{
dp[i]=max(dp[i-1],dp[i-2]+money[i]);
}
}
return dp[n-1];
}
int main(){
int n;
cin>>n;
vector<int> money;
vector<vector<int> > group;
int i;
int tem=n;
vector<int> res;
int a[50];
while(tem!=0){
cin>>a[tem];
while (cin>>i){
money.push_back(i);
if(cin.get()=='\n') break;
}
group.push_back(money);
money.clear();
tem--;
}
while(tem!=n){
res.push_back(rob(group[tem]));
tem++;
}
vector<int>::iterator it;
for(it=res.begin();it!=res.end();++it)
cout<<*it<<endl;
return 0;
}
|
地宫取宝
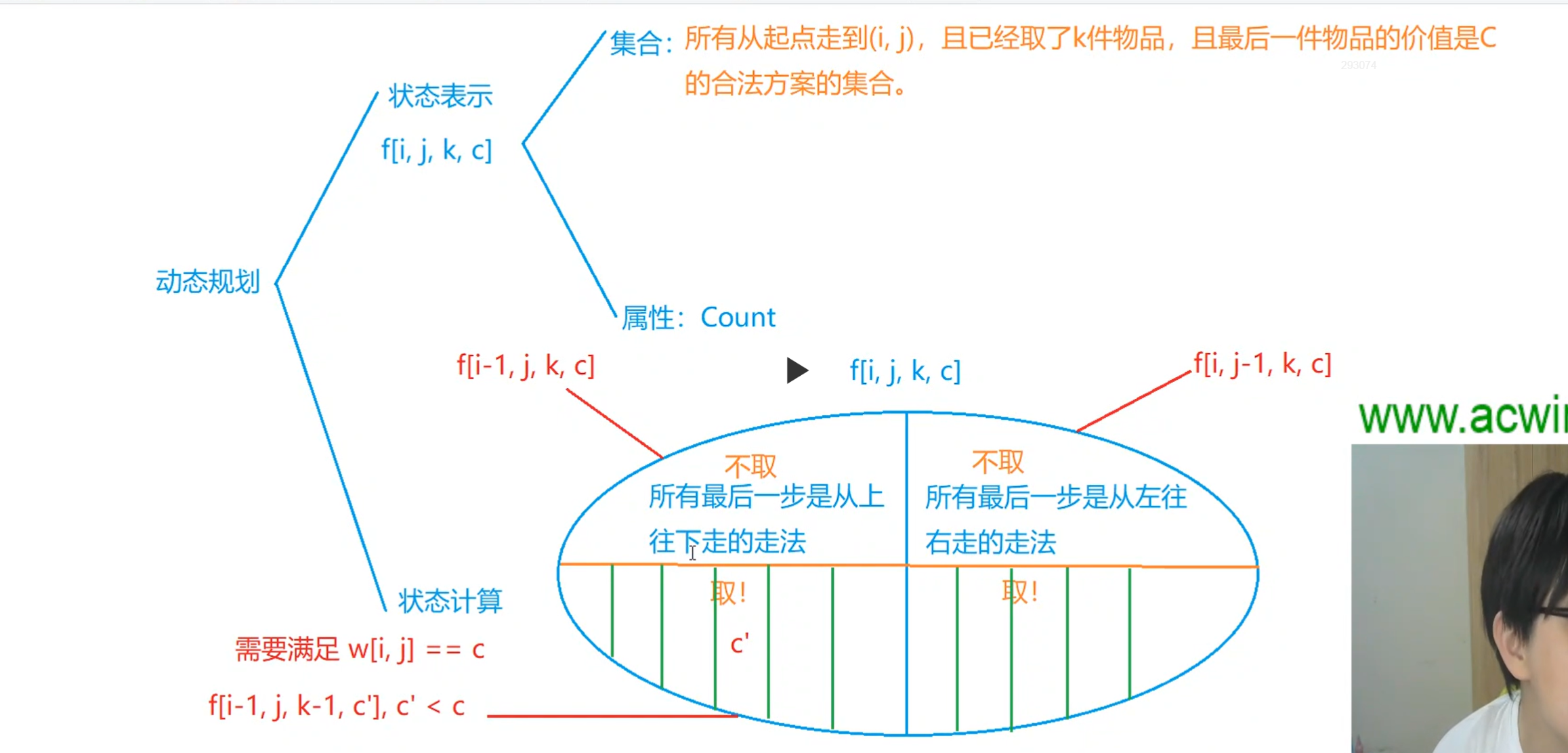
X 国王有一个地宫宝库,是 n×m个格子的矩阵,每个格子放一件宝贝,每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。
小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是 k
件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这 k件宝贝。
输入格式
第一行 3
个整数,n,m,k
,含义见题目描述。
接下来 n
行,每行有 m
个整数 Ci
用来描述宝库矩阵每个格子的宝贝价值。
输出格式
输出一个整数,表示正好取 k
个宝贝的行动方案数。
该数字可能很大,输出它对 1000000007
取模的结果。
数据范围
1≤n,m≤50
,
1≤k≤12
,
0≤Ci≤12
![]/img/(image-4.png)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| #include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=55, MOD =100000007;
int n,m,k;
int w[N][N];
int f[N][N][13][14];
int main(){
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>w[i][j];
w[i][j]++;
}
}
f[1][1][1][w[1][1]]=1;
f[1][1][0][0]=1;
for(int i=1;i<=n;i++){
for(int j=0;j<=m;j++){
for(int u=0;u<=k;u++){
for(int v=0;v<=13;v++){
int &val=f[i][j][u][v];
val=(val+f[i-1][j][u][v])%MOD;
val=(val+f[i][j-1][u][v])%MOD;
if(u>0&& v==w[i][j]){
for(int c=0;c<v;c++){
val=(val+f[i-1][j][u-1][c])%MOD;
val=(val+f[i][j-1][u-1][c])%MOD;
}
}
}
}
}
}
int res=0;
for (int i=0;i<=13;i++) res=(res+f[n][m][k][i])%MOD;
cout<<res;
return 0;
}
|




